Understanding the nuances of C# Collections
This article is based on .NET 9 and C# 13. I aim to cover the behaviors of common collections within the System.Collections.Generic namespace.
Insertion behaviors in Dictionary
The Dictionary<TKey, TValue> provides a mapping from a set of keys to a set of values. Values can be inserted into a dictionary with varying behaviors. Insertion in a Dictionary is implemented by the private method TryInsert. This method accepts an additional parameter behavior, which is an enum with values IgnoreInsertion, OverwriteExisting, and ThrowOnExisting. Consider the following code, where each operation behaves differently:
Dictionary<int, int> dict = new Dictionary<int, int>();
dict[1] = 3; // Calls underlying private method TryInsert with behavior OverwriteExisting
Debug.Assert(dict[1] == 3);
dict.TryAdd(1, 5); // Calls underlying private method TryInsert with behavior IgnoreInsertion
Debug.Assert(dict[1] == 3);
dict.Add(1, 4); // Calls underlying private method TryInsert with behavior ThrowOnExisting
The Curious case of 'Capacity' and 'Count'
The Dictionary also exposes two properties: Count and Capacity. Count denotes the number of key-value pairs in the dictionary, and Capacity denotes the size of the underlying container that holds the dictionary. The Capacity property was only exposed from .NET 9 and is not available in older versions of .NET. We can specify the value for Capacity in the constructor: Dictionary<int, int> dict = new Dictionary<int, int>(5);, which will create an underlying container of size 7. Why size 7? Initially, I was puzzled too, so I checked the source code of the Dictionary implementation.
The size is 7 because .NET uses a prime array, and the code selects the smallest prime number from the array that is larger than the given capacity. Here is the prime array for reference:
internal static ReadOnlySpan<int> Primes =>
[
3, 7, 11, 17, 23, 29, 37, 47, 59, 71, 89, 107, 131, 163, 197, 239, 293, 353, 431, 521, 631, 761, 919,
1103, 1327, 1597, 1931, 2333, 2801, 3371, 4049, 4861, 5839, 7013, 8419, 10103, 12143, 14591,
17519, 21023, 25229, 30293, 36353, 43627, 52361, 62851, 75431, 90523, 108631, 130363, 156437,
187751, 225307, 270371, 324449, 389357, 467237, 560689, 672827, 807403, 968897, 1162687, 1395263,
1674319, 2009191, 2411033, 2893249, 3471899, 4166287, 4999559, 5999471, 7199369
];Now, with the size being 7, when we insert the 8th item into the Dictionary, .NET needs to resize the underlying container. For resizing, .NET first computes twice the current count and then finds the first prime number from the array that is larger than this value. In this example, it is 7 * 2 = 14, and the next prime in the list is 17. Therefore, after inserting the 8th item, the capacity of the dictionary will be 17.
Also, if you know the size of the data in advance, specifying the capacity can provide a minor performance boost. Please see the benchmark results below for Dictionary insertion.
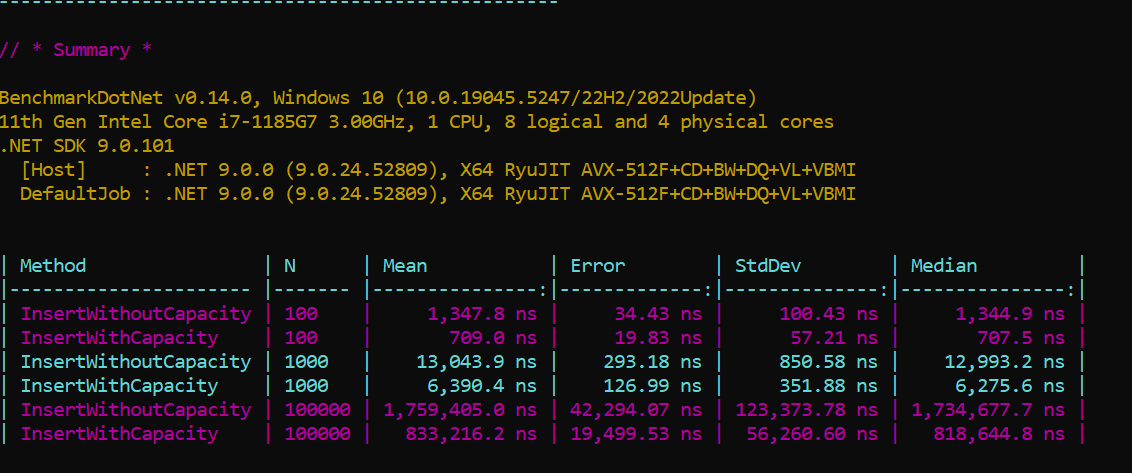
HashSet and OrderedDictionary also behave in the same way with respect to capacity and resizing.
For Stack<T>, Queue<T>, SortedList<TKey, TValue>, and List<T>, resizing is not based on the prime array. In these cases, the container is created with the given capacity in the constructor, and for resizing, the size is simply doubled. Consider the example: Stack<int> ints = new Stack<int>(5);. After pushing the 6th item, the size is doubled to 10.
PriorityQueue<TElement, TPriority> works similarly to Queue<T> and List<T>, but the property Capacity is not yet exposed.
Final Note
Understanding the inner workings of collections in C# can greatly enhance your ability to write efficient and effective code. As we've seen, the Dictionary<TKey, TValue> class in .NET 9 has some interesting behaviors, particularly with how it handles capacity and resizing. By leveraging the prime number array for sizing, .NET ensures that the hash table's performance remains optimal.
Remember that specifying the initial capacity can lead to performance gains, especially when the size of the dataset is known beforehand. This is because it minimizes the number of resizes that need to occur as the collection grows.
While Dictionary<TKey, TValue>, HashSet<T>, and OrderedDictionary use prime numbers to determine their capacities, other collections like Stack<T>, Queue<T>, SortedList<TKey, TValue>, and List<T> follow a simpler doubling strategy. This knowledge allows you to predict and control the memory usage and performance characteristics of your collections more accurately.
Happy coding!